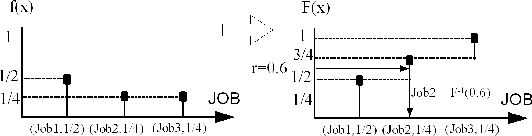Probability Mass Function

A template class RVofPMF<T> is used for generating a random number of a probability mass function (PMF). This class has the probability table pmf which is Dictionary<T, double> whose key is T-typed object and value is the probability of occurrence for the key. The function SampleV() returns T-typed key whose cumulative pmf value is firstly greater than a random number r in uniform[0, 1].

    public class RVofPMF<T> : Random
    {
        //-- pairs of (T, probability)
        public Dictionary<T, double> pmf;
        public RVofPMF() : base() {...}
        public T SampleV() {...}
    }

Figure 2.3: PMF $f(s)$ and its cumulative function $F(x)$

Figure 2.3 shows how RVofPMF::SampleV() works. Let's assume that there are three kinds of jobs, Job1, Job2, and Job3 coming into a system with their corresponding probabilities 0.5, 0.25, and 0.25, respectively. To pick one of them, we generate a random number $r$ in the uniform PDF [0, 1]. Let's say $r=0.6$ at this time. Then, since the inverse function of $F(0.6)$ that is the cumulative function of $f(x)$ is Job2, Job2 will be picked at this moment.

For this example, the user should fill out the table pmf as pmf={(Job1, 0.5), (Job2, 0.25), (Job3, 0.25) } before calling SampleV() function. Of course, summation of values pmf[key] for all keys should be 1 for being a correct PMF function.

We will see an application of RVofPDF and RVofPMF when we take a look at Generator class in Section 4.2.1